The Volume of a Prism and Cylinder
Page 1
***Use geometric definitions page in the previous post to find definitions***
The volume of a prism can be found using the formula: V= (area of base)(height)
Page 1: Example
216 cm^3
36 cm^3
Page 2
b 339 cm^3
c about 60
The Volume of a Sphere
Page 1
The height of the can is 6 cm and the diameter of the can is 6 cm
The diameter of the tennis ball is 6 cm.
Notice that the diameter and height of the cylinder are equal to the diameter of the sphere.
If the water that spilled out of the can is measured, you will notice that it is two thirds of the water that was originally in the can.
The volume of the ball is 2/3 the volume of the can.
Page 2
The volume of a sphere = 2/3 x Volume of a cylinder into which the sphere just fits
or
The volume of a sphere =
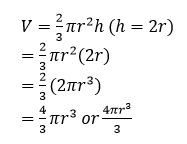
Page 2: Practice
Cylinder V= 785.3981634 or 785.4 cm^3; Sphere V= 523.5987756 or 523.6 cm^3
1436.75504 or 1436.8 cm^3
a) 3811cm^3
Page 6
17. c) 5.5 cm
18. d) 10 cm x 10 cm x 10 cm
21. No
Page 7: 2.6 Global Proportions
65449.84695 or 65449.8 cm^3
b i) 125000 cm^3
b ii) 59550.15305 or 59550.2cm^3
Continuum and Connections—Perimeter, Area, and Volume, pg. 12
Page 1
Volume of the box of birdseed: 9000 cm^3
Volume of the bird feeders: 1005.309649 cm^3 (Do not round this answer because who will need it to calculate how many cylindrical bird feeders you can fill)
Mario can fill 8.95246555 or 9 bird feeders.
Find 2 different ways to find the area of this patch of pavement:
Calculate the area of the patch of pavement using the trapezoid formula
Calculate the area of the patch of pavement by dividing it into a rectangle and triangle
Calculate the area of the path of pavement by dividing it into three triangles and using the Pythagorean theorem
Page 2
The volume of the cone on the left is 6.283185307 or 6.3 cm^3
The volume of the cone on the right is 4.71238898 or 4.7 cm^3
The volumes are not the same.
The height of the aquarium is 35 cm.